#2 삽입정렬

카드 정렬 문제

쉽게 말해서 카드 놀이를 할 때 손에 쥔 카드를 정렬하는 것과 방법이 같다.
탁자에 쌓여있는 카드를 한장씩 가져와 숫자의 순서대로 왼손에 쥐게되는 경우를 생각해보자.
카드를 삽입할 적절한 위치를 찾기 위해 그림과 같이 왼손에 이미 든 카드와 새 카드를 오른쪽에서 왼쪽방향으로 차례로 비교하면서 삽입 할 위치를 찾게 된다 탁자에 있던 모든 카드를 다 왼손에 쥐고있을 경우 이 카드들은 순서대로 정렬이 되어 있을것이다. 이게 삽입정렬이다.

삽입정렬 - Insertion sort

def insertionSort():
    arrayA = [5, 2, 4, 6, 1, 3]
    # 첫번째 열은 루프를 돌 필요가 없음
    for j in range(1, len(arrayA)):
        i = j - 1
        key = arrayA[j]
        
        # 검사식
        while i >= 0 and arrayA[i] > key:
            arrayA[i + 1] = arrayA[i]
            i -= 1
        arrayA[i + 1] = key
    
    print(arrayA)
    # 출력 : [1, 2, 3, 4, 5, 6]

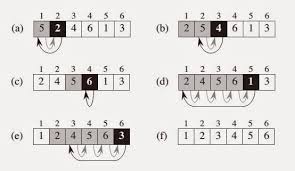
위의 그림에서 검은색 사각형은 arrayA[j]의 값을 의미하며, 검사식에서 회색 사각형에 있는 값들과 오른쪽부터 차례로 비교한다.
회색 사각형의 값이 더 클 경우 한 칸씩 오른쪽으로(검은색 사각형의 위치)로 이동하며 각 인덱스마다 반복해서 최종적으로 정렬된 값을 얻을 수 있다.

루프 불변성

루프 불변성(Loop Invariant)

책에는 조금 설명이 어렵게(내가 난독증 일 수도 있다) 되어 있길래 조금 더 간략하게 정리해본다.

루프 불변성(Loop invariant) 이란 알고리즘을 수행하면서 변하지않는 특성(statement)을 말하며 프로시저가 종료될 때까지 계속해서 유지되어야 하는 특성을 말한다.
작성된 알고리즘이 타당한 알고리즘인지를 증명하는 방법 중 하나이며 3단계의 조건을 만족시키면 완성적인 알고리즘이다라고 할 수 있다.
삽입정렬에서의 항상 만족해야하는 특성이라고하면 ‘0부터 j-1까지의 원소들은 입력 배열에서 0부터 j-1까지 있던 원소들이고 모두 정렬되어있다‘로 정의할 수 있다.

각 단계별로 조건과 만족하는지를 직접 확인해보자.

Initialization(초기조건)

루프가 시작되기 전 특성을 만족하는가?

위의 코드에서 for-loop의 j = 1로 초기화 된 직후에 조건을 만족하는지 확인해보자.

1. 0 ~ j-i까지의 열은 즉 j = 1인 시점이니까 0번 하나만 존재하는 부분배열을 말한다.
2. 부분배열 arrayA[0 … j-1]은 현재 값이 하나이므로(arrayA[0] 하나만 존재한다) 정렬되어 있다.
3. 부분배열 arrayA[0 … j-1]은 arrayA[0 … j-1]까지의 배열(입력배열)에서 있던 값이다.
4. 따라서 Loop invariant를 만족한다.

Maintenance(유지조건)

루프의 다음 반복이 시작되기 전(루프가 돌고 있는 모든)에도 특성을 만족하는가?

1. while-loop에서 arrayA[j]의 적절한 위치를 찾기위해 arrayA[j - 1], arrayA[j - 2] …을 오른쪽으로 하나씩 shift한다.
2. 적잘한 위치에 arrayA[j]를 넣는다.
3. 위의 특성 증 arrayA[0 … j-1]까지의 배열은 모두 정렬되어 있는 상태이다.
4. 물론 입력배열 arrayA[0 … j-1]의 부분배열이다.
5. 따라서 Loop invariant를 만족한다.

Termination(종료조건)

루프가 종료되었을 때 특성을 만족하는가?

1. for-loop의 j값이 length가 되면서 loop를 종료한다.
2. 현재 j값이 length이므로 j - 1은 배열의 끝이되고 0번부터 끝(전체 배열)이 된다.
3. 0 - j - 1까지의 원소들은 물론 원래의 입력배열에서 존재하던 값이다.
4. 출력으로 나온 전체 배열이 정렬되어 있는 상태이다.
5. 따라서 Loop invariant를 만족한다.